May 2024
The many locations for space science missions
Introduction
The space science enabled by Teledyne’s visible and infrared focal plane arrays depends on successful launch and orbit insertion of the spacecraft. The orbit is one of the most important choices made by a science mission. There are several options for an orbit in space and this article provides information about the most used satellite orbits. Science satellite orbits fall into three categories:
-
Earth orbits
-
Low Earth Orbit (LEO) and Sun-Synchronous Orbit (SSO)
-
Medium Earth Orbit (MEO)
-
Geosynchronous Earth Orbit (GSO) and Geostationary Earth Orbit (GEO)
-
Highly Elliptical Orbit (HEO)
-
Sun-Earth Lagrange Point Orbits
-
Locations where the Sun’s and Earth’s gravity combine to produce a satellite orbit about the Sun that matches the time that it takes the Earth to complete one orbit around the Sun: 365 days, 6 hours, and 9 minutes.
-
Interplanetary Orbits
Before we discuss these orbits, it is useful to review the basics principles and mathematics of orbital mechanics.
An introduction to orbital mechanics
The physics of gravitational orbits was formulated by Isaac Newton over 300 years ago. Sir Isaac Newton (1642 – 1727) was an English polymath who contributed to many fields including mathematics, physics, and astronomy. In the field of optics, he built the first successful reflecting telescope, and he developed a sophisticated theory of the colors of light based on his observation that a prism separates white light into a spectrum of colors. In his pioneering book entitled Mathematical Principles of Natural Philosophy, Isaac Newton formulated the laws of motion and universal gravitation that became the dominant scientific viewpoint until the Newtonian laws of motion were superseded by the theories of special and general relativity proposed by Albert Einstein in 1905 and 1915. Isaac Newton is considered one of the greatest and most influential scientists in history.

Portrait of Isaac Newton, 1689 (age 46)
Courtesy: Isaac Newton Institute
While the Global Positioning System (GPS) must account for both special and general relativity to deliver position / time accuracies of 1-meter / 100 nsec, Newtonian theory provides a very good description of the motions of satellites used for space science. Newton’s law of universal gravitation states that gravity is an attractive force that exists between all objects that have mass. For the case of two objects, the magnitude of the gravitational force is directly proportional to the masses (M1, M2) of the two objects and inversely proportional to the square of the distance (r) between the two objects. The equation for gravitational force (F) is:
(1)
The masses (M) are expressed in kilograms (kg), G is the universal gravitational constant, and distance (r) is expressed in meters. The gravitational constant is: G = 6.67 × 10-11 N•m2/kg2. The unit N stands for Newton, which is the international unit of force where 1 N = 1 kg•m/sec2. (The unit of force is aptly named after Isaac Newton.)
-
Note that the distance r is measured from the center of mass of the objects, so that when equation (1) is used for satellites orbiting the Earth, r refers to the distance from the center of the Earth.
According to Newton’s first law of motion, an object that is in motion will continue its motion in a straight line, unless compelled to change its motion by a force exerted upon it. For an object in a uniform circular orbit of radius r and moving at velocity v, the object must be accelerated by a force directed to the center of the circular orbit. The acceleration (a) has a magnitude given by:
(2)
Since according to Newton’s second law of motion, the acceleration (a) of an object with mass M, is related to force (F) by the equation F = M × a, we can determine the velocity (v) of a satellite with mass msat in a circular orbit around the Earth at distance r (from the center of the Earth).
(3)
Equation (3) can be used to determine the orbital period and velocity of Earth orbiting satellites as a function of altitude above the Earth’s surface. Some examples are provided in the table below. Note that the orbital altitude is referenced to the Earth’s radius at the equator: 6,378.1 km.
Table 1: Satellite Orbit Velocity and Period as function of altitude above the Earth
Orbit Altitude
(km) |
Orbital Velocity
(km/sec) |
Orbit Period
(min) |
Orbit Period
(hour) |
Comments |
| 200 |
7.78 |
88.5 |
1.47 |
|
| 370 |
7.69 |
91.9 |
1.53 |
Low end of ISS orbit |
| 400 |
7.67 |
92.6 |
1.54 |
|
| 460 |
7.63 |
93.8 |
1.56 |
High end of ISS orbit |
| 600 |
7.56 |
96.7 |
1.61 |
|
| 1,000 |
7.35 |
105.1 |
1.75 |
|
| 2,000 |
6.90 |
127.2 |
2.12 |
|
| 5,000 |
5.92 |
201.3 |
3.36 |
|
| 10,000 |
4.93 |
347.7 |
5.79 |
|
| 15,000 |
4.32 |
518.5 |
8.64 |
|
| 20,000 |
3.89 |
710.6 |
11.84 |
|
| 20,230 |
3.87 |
719.9 |
12.00 |
GPS satellites |
| 29,429 |
3.34 |
1,123.9 |
18.73 |
|
| 35,786 |
3.07 |
1,436.1 |
23.9345 |
GSO satellites |
| 385,000* |
1.02 |
39,340.8 |
655.68 |
Moon orbits in 27.32 days |
ISS = International Space Station
GPS = Global Positioning System
GSO = Geosynchronous Earth Orbit
*Average distance of Moon from the Earth's center
-
Orbit altitude refers to the distance above the Earth at the equator where the Earth’s radius is 6,378.1 km.
-
Note that the Earth is a slightly oblate spheroid with the radius at the poles (6,356.7 km) 20.4 km smaller than at the equator. The Earth’s oblateness is quite valuable in making orbits that are sun-synchronous, as discussed in the section on Earth orbits.
-
The Earth and Moon orbit about their barycenter (common center of mass) which lies about 4,670 km from the Earth’s center (about 73% of the Earth’s radius), forming a satellite system called the Earth-Moon system.
The second to last value in Table 1 is a very special orbit. With orbital altitude of 35,756 km (above the Earth’s surface), this is the altitude of Geosynchronous Earth Orbit (GSO) satellites. At the GSO altitude, a satellite’s orbital period matches the Earth’s rotation: 23 hours, 56 minutes, and 4.09 seconds, which is termed one sidereal day.
Eccentricity of Elliptical Orbits
All orbits of one body about another body are ellipses. An ellipse is an oval shape with two foci, with each foci equally distant from the center of the ellipse. On the ellipse, the sum of the distances from the two foci is a constant value which equals 2a in the drawing below. The parameters defining an ellipse are:
- origin (o)
- semi-major axis (a)
- semi-minor axis (b)
- distance of foci from center (c)
- eccentricity (e=c/a)
Eccentricity is the distance of a focus from the center of the ellipse divided by the semi-major axis. A circular orbit is the special case of an ellipse where the two foci and origin of the ellipse are coincident. For a circular orbit, c = 0 and the eccentricity is zero.
For a small body orbiting a large body, the large body is located at one of the two foci of the ellipse. The location on the ellipse when the orbiting body is closest to the large body is called the perigee. The far end of the orbit (at the other end of the ellipse) is called the apogee.
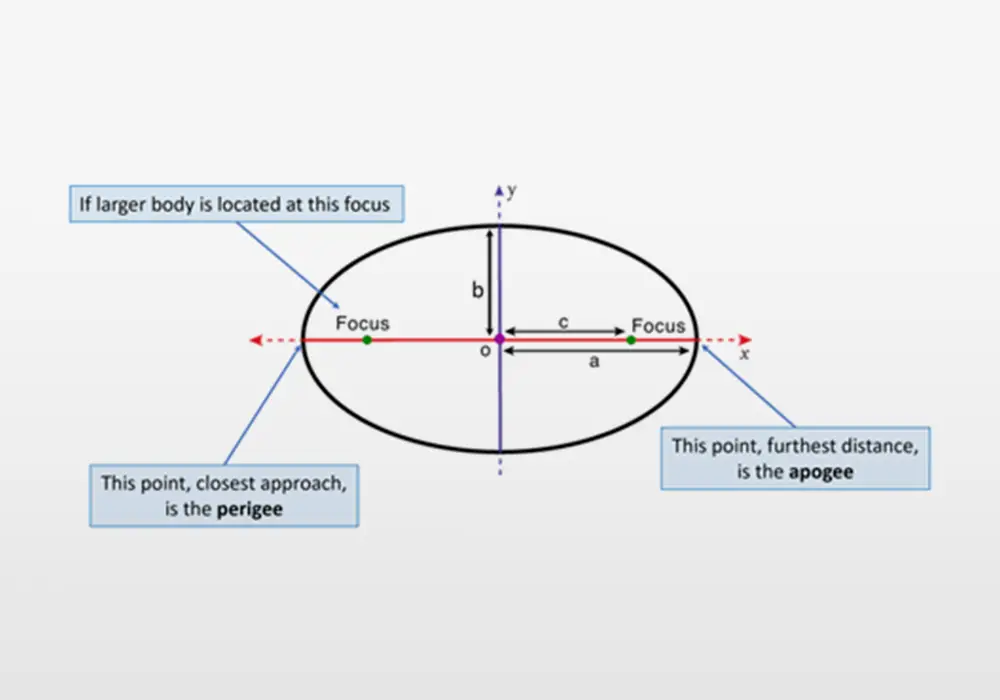
Figure of an ellipse
Credit: Teledyne
The instantaneous velocity of a small body in an elliptical orbit around a large body is given by:
(4)
where G is the universal gravitational constant, and distance (r) is the distance (expressed in meters) of the satellite from the ellipse focus where the large body resides, a is the semi-major axis, and M is the mass of the large object that is being orbited. Equation (4) collapses to equation (3) for circular orbits for which r is always equal to a.
The period of a satellite in an elliptical orbit depends only on the semi-major (longest) axis of the ellipse. The animation below shows five elliptical orbits that have the same semi-major axis with eccentricities ranging from 0.0 to 0.8. The period is the same for all five orbits, but the variation in speed greatly increases for higher values of eccentricity.
The Earth's motion through the Universe
Everything in the universe is being gravitationally attracted by something else. It is interesting to list the motions of the Earth in the Universe at increasingly larger scales.
-
On Earth, at the equator, the Earth’s rotation speed is 0.465 km/sec (465 m/sec or 1,040 mph).
-
The Earth is orbiting the Sun at an average speed of 29.8 km/sec (66,661 mph).
-
The Sun (and with it, the Solar System) is orbiting the center of the Milky Way galaxy at a speed of 222 km/sec (496,600 mph).
-
On a larger scale, the Milky Way galaxy is being gravitationally attracted to a region called the “Great Attractor” in the center of the Laniakea Supercluster at a speed of 600 km/sec (1.34 million mph).
One way that astronomers find exoplanets in the Milky Way is by observing the wobble of stars due to the gravitational pull of an exoplanet on its star. The star and its exoplanet orbit about their barycenter, causing the star to move towards and away from the Earth. The “Doppler shift” of wavelengths absorbed in the star’s atmosphere is most pronounced if the exoplanet orbital plane is seen edge-on from Earth. The most accurate exoplanet Doppler measurement instruments on ground-based telescopes can measure stellar velocities with an accuracy better than 1 m/sec (0.001 km/sec). To be useful, the Doppler measurement data reduction must very accurately remove four velocities that affect the relative motion of the Earth to the star:
-
The Earth’s rotation (up to 0.465 km/sec)
-
The Earth’s orbit about the Sun (up to 29.8 km/sec)
-
The solar system’s motion through the Milky Way (up to 222 km/sec)
-
The exoplanet’s host star motion through the Milky Way (up to hundreds of km/sec)
All of these velocities must be computed in three-dimensional space about the vector from the telescope’s location on Earth to the star-exoplanet system. It is remarkable how well these corrections are made. The animation below shows the wobble detected by astronomical instrumentation, the majority of which use Teledyne’s visible or infrared focal plane arrays.
A star and its companion planet both orbit the barycenter (center of mass), which results in a small "wobble" of the star (top left). When viewed edge-on (bottom left), the star moves periodically towards and away from an observer (in the direction in and out of the page). This radial speed (top right) can be measured using doppler spectroscopy, which is a technique that splits the star's light into a spectrum of different colours. Absorption lines in the spectrum are due to chemicals in the star's atmosphere, and their exact colors are determined by the chemical structure. The radial speed of the star causes a doppler shift of the star's light, which can be detected if the absorption lines are different from their expected value (bottom right).
Credit: Alysa Obertas (own work, 12 July 2022)
This image is licensed under the Creative Commons Attribution-Share Alike 4.0 International license.
Example of a Three-Body System
The orbits discussed thus far are for two bodies. When one body is much more massive than the other, we only need consider the mass of the larger body. In many cases, the masses of both bodies must be considered since the two bodies will orbit about their barycenter (center of mass). A much more difficult mathematical situation is when three bodies are involved, such as when a small spacecraft travels between the Earth and the Moon.
The plot below shows the gravitational potential of the Earth-Moon system and how the potential affects a spacecraft (which has negligible mass compared to the Earth and Moon).
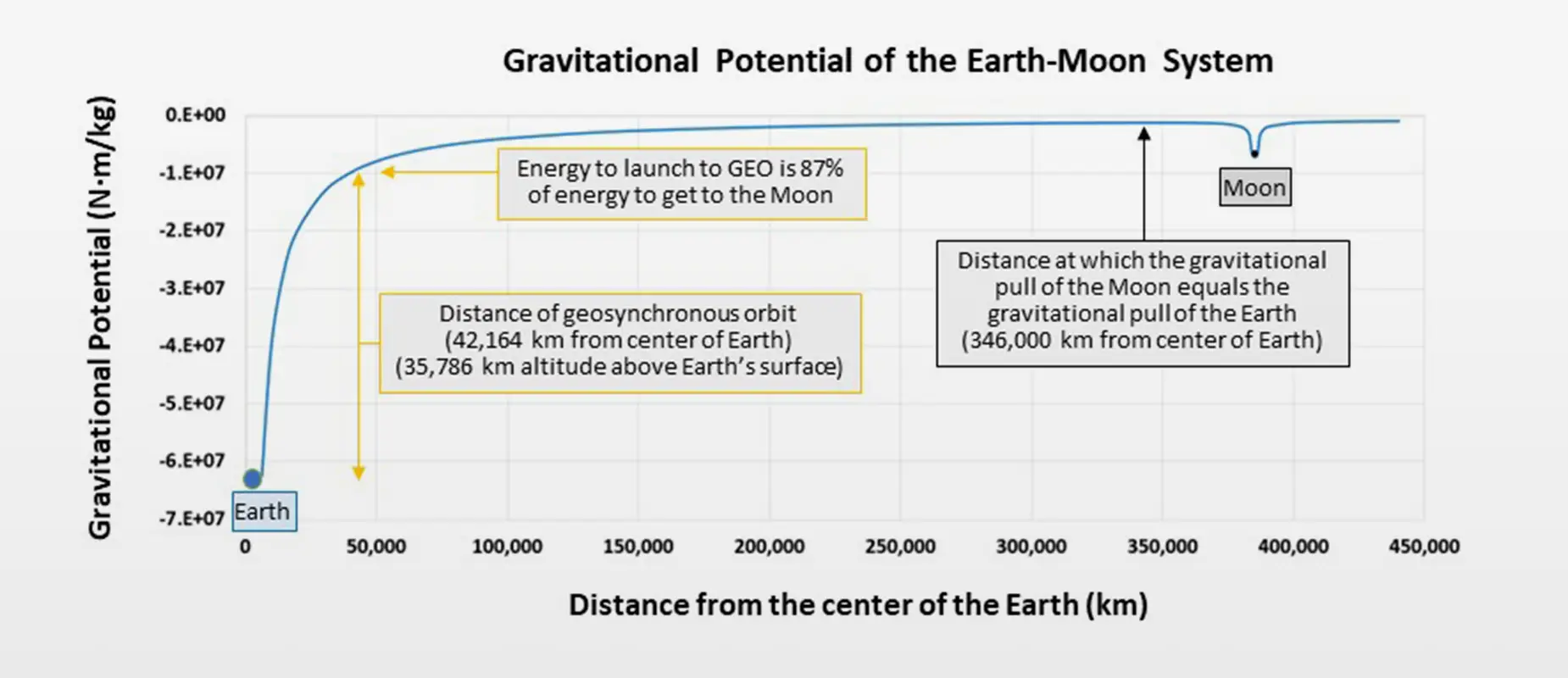
Gravity Potential of the Earth-Moon system
Credit: Teledyne
Comparison of the Earth and Moon
Table 2: Comparison of the Earth and Moon
| |
Earth |
Moon |
Ratio
(Moon/Earth) |
| Equatorial Radius (km) |
6378.1 |
1738.1 |
27.3% |
| Volume (km3) |
1.083 x 1012 |
2.197 x 1010 |
2.03% |
| Mass (kg) |
5.972 x 1024 |
7.346 x 1022 |
1.23% |
| Density (g/cm3) |
5.51 |
3.34 |
60.6% |
The Moon’s radius is slightly larger than one-quarter of the Earth’s radius but the Moon’s mass is only 1.23% of the Earth. This is due to the Moon’s smaller volume (volume = (4/3) · π · radius3) and lower density (60.6% of the Earth’s density).
Inclination of spacecraft in orbit about the Earth
Satellites that orbit Earth are in a plane that is tilted relative to the Earth’s equator. As shown in the figure below, the orbital inclination is the angle between the plane of the orbit and the equator. An orbital inclination of 0° is directly above the equator and inclination of 90° crosses directly over the Earth’s north and south poles. An inclination of 180° orbits above the equator in the direction opposite the Earth’s spin. Orbits with inclination angle between 90° and 180° are called a retrograde orbit.
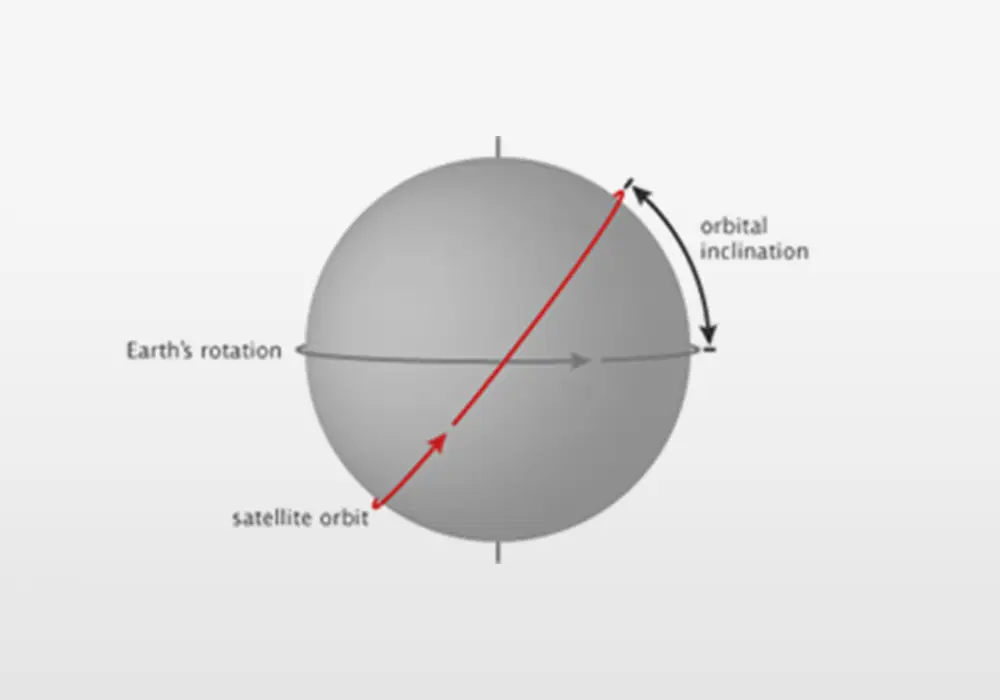
Orbital inclination of a satellite
Credit: (NASA illustration by Robert Simmon)
The inclination of a satellite orbit at launch must be equal to or greater than the latitude of the launch site. (After launch the orbit inclination can be reduced and often is for MEO and GEO. But typically the orbit inclination is not reduced for LEO satellites due to the large amount of energy required.) An example orbit is the International Space Station (ISS). The ISS orbit has an inclination of 51.6°. This inclination angle is greater than the latitude of the two launch sites that service the ISS: Kennedy Space Center (28.574° N) and Baikonur Cosmodrome (45.965° N). The 51.6° inclination angle also enables the ISS to fly over 90% of the inhabited Earth. The figure below shows the portion of the Earth that the ISS flies over.
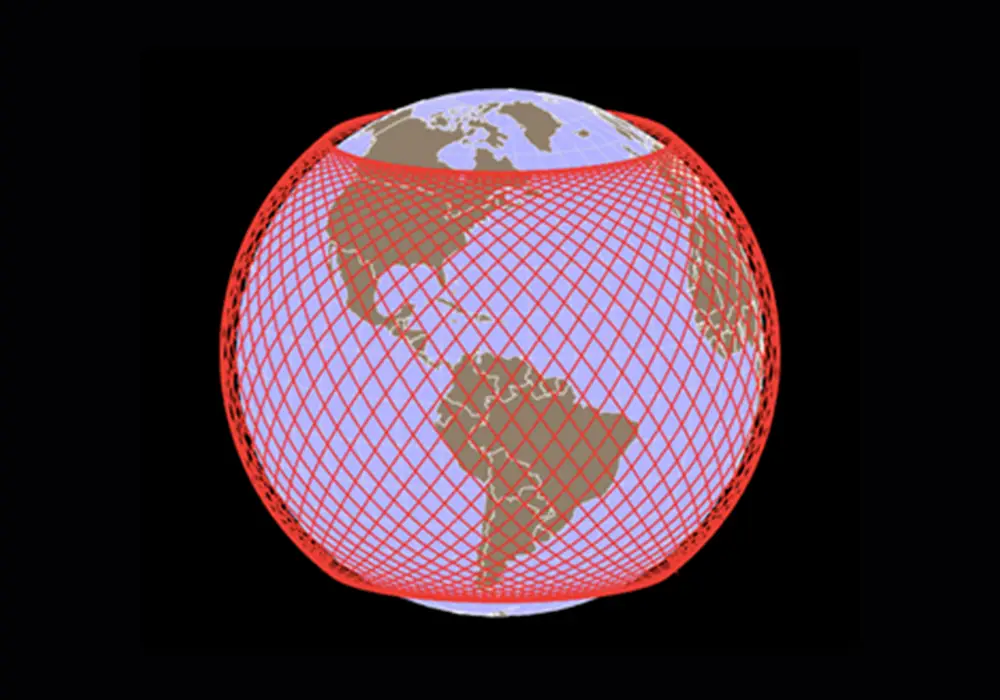
International Space Station orbits: 51.6° inclination
(Figure Credit: engagingdata.com)
Even though the strict mathematical definition of a polar orbit is one with inclination of 90°, orbits with inclinations of 60° to 120° are often referred to as polar orbit satellites. The advantage of polar orbit for LEO satellites is that a polar orbit enables the satellite to be able to view a larger fraction of the Earth.
Earth Orbits
The altitudes of the most popular satellite orbits are shown in the figure and animation below. The figure and animation are drawn to scale with the appropriate relationship between orbital speed and altitude in the animation.
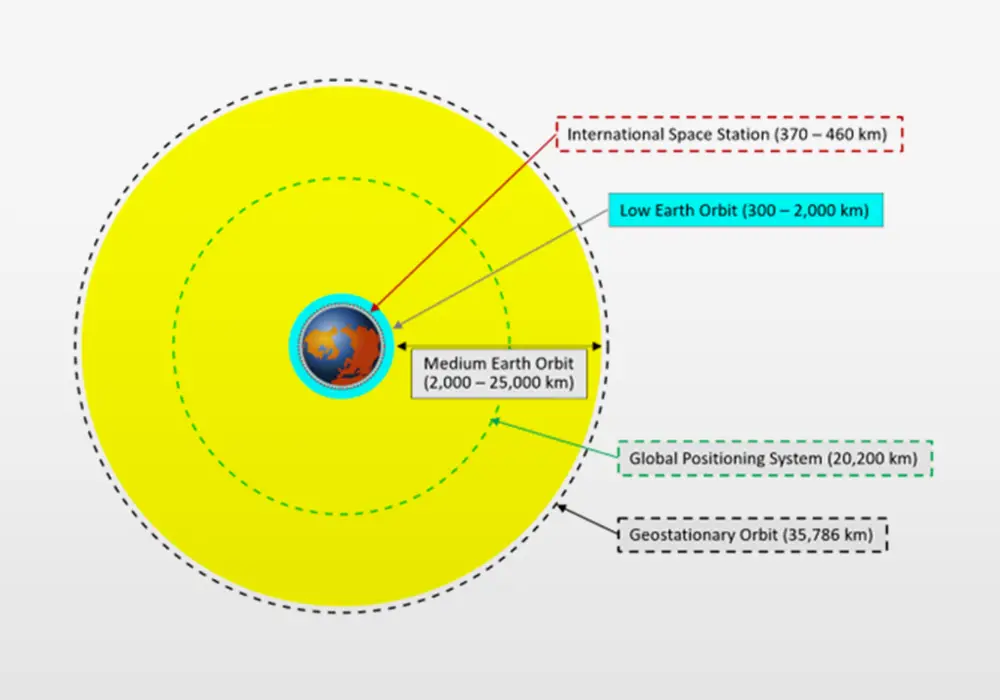
Earth orbits graphic
Credit: Public domain
Earth orbits
Courtesy: Public domain
Low Earth Orbit (LEO)
Low Earth orbit (LEO) generally refers to orbital altitudes of 300 to 2,000 km. At lower altitudes, atmospheric drag necessitates frequent boosting of altitude. But very low Earth orbit, or VLEO, is being promoted by the European Space Agency and some private companies because VLEO (at 100 to 300 km altitude) is easier to access and enables smaller satellites with smaller optics.
According to the website Orbiting Now (https://orbit.ing-now.com), as of March 14, 2024, there are 8,221 satellites in low Earth orbit (over 90% of all active satellites). LEO has several advantages:
-
LEO requires the least energy to reach
-
See figure on the Gravitational Potential of the Earth-Moon system
-
Radio signal propagation takes less time and consumes less power
-
A given aperture size achieves better spatial resolution on the Earth
LEO also enables a special type of orbit called a sun synchronous orbit (SSO). An SSO is a polar orbit for which the satellite passes over any given point on the Earth at the same time (termed local mean solar time). A sun-synchronous orbit is very useful for imaging, reconnaissance, and weather satellites because every time the satellite is overhead, the solar illumination angle on the Earth is nearly the same. This consistent lighting enables scientists to better quantify changes of the Earth’s surface and vegetation. To maintain the constant solar illumination, the satellite orbit must precess through one complete revolution each year, so that it maintains the same relationship with the Sun. This precession is enabled by the oblate spheroid shape of the Earth. The fact that the Earth is slightly fatter at the equator causes polar orbits with inclination angle less than 90° to precess to the West, and polar orbits with inclination angles greater than 90° to precess toward the East. To maintain synchronicity with the Sun, the precession needs to be eastward, and thus inclination angles of 96° to 105° (slightly retrograde) are required for sun-synchronous orbits. Precession rate depends on altitude with the optimal orbit inclination angle shown in the figure below.
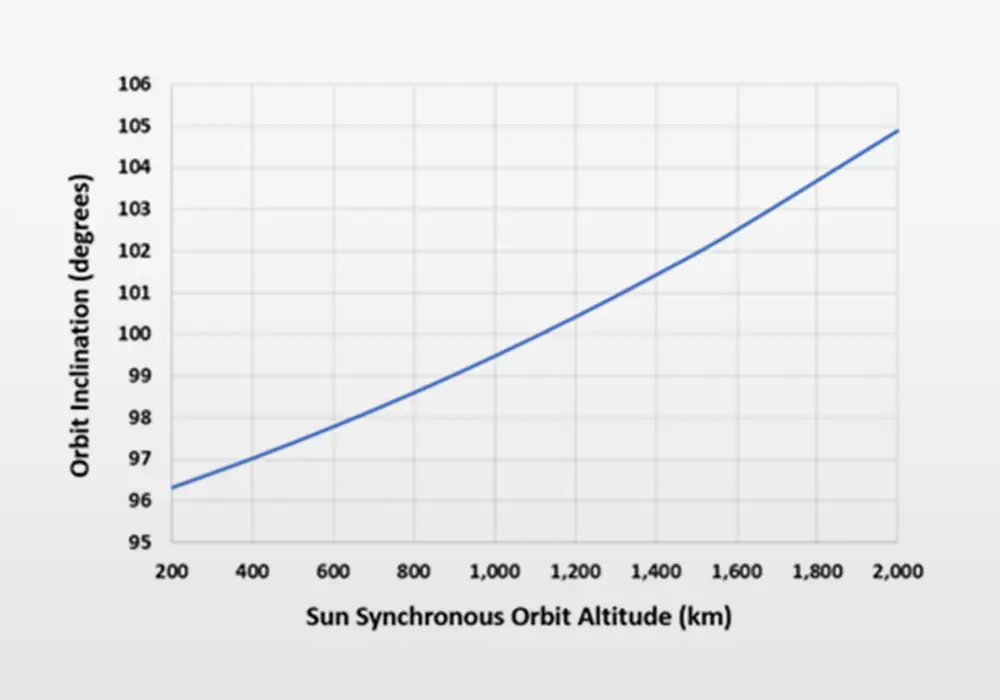
Sun-Synchronous Orbit Inclination Angle versus Orbit Altitude
Courtesy: Teledyne
Since most polar orbits are sun-synchronous and SSO inclination angles range from 96⁰ to 105°, SSO orbits leave a hole without satellites at the north and south poles. See figure below that shows multiple orbits of a 98° inclination polar orbit.
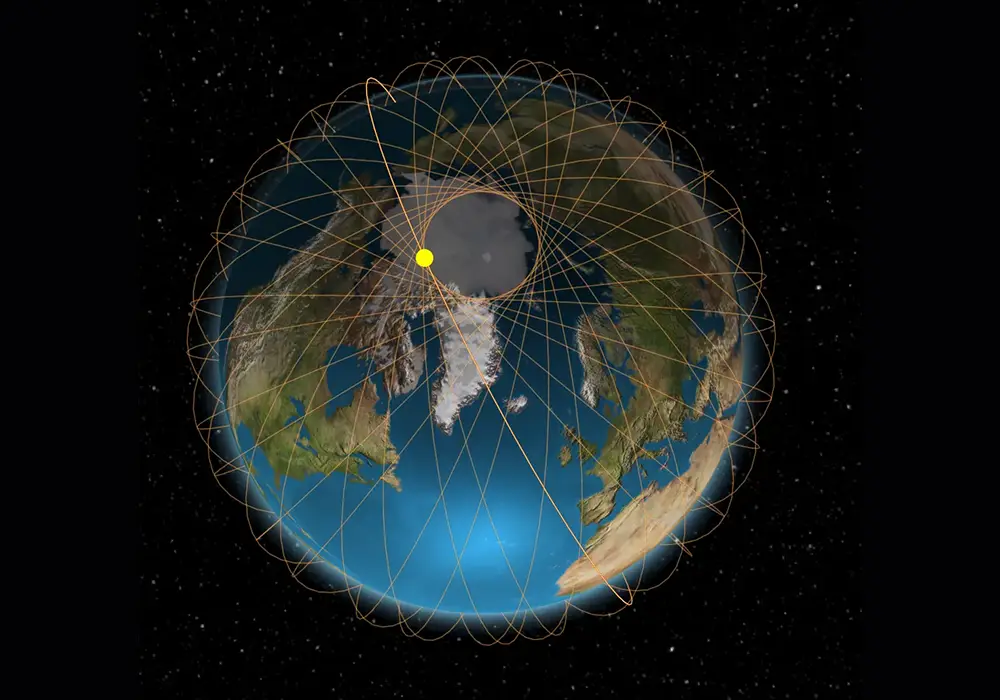
Orbital path of a satellite in example SSO (98 degree inclination at 700 km altitude)
Credit: LeoLabs
The SSO satellites also tend to bunch up and create “traffic hot spots” in the region 7 to 15 degrees from the north and south poles. This bunching increases the likelihood of a satellite collision. More close approaches occur near the north and south poles than anywhere else in space.
Medium Earth Orbit (MEO)
Medium Earth Orbit (MEO) altitude ranges from LEO to the geosynchronous orbit (GSO) altitude of 35,786 km. A typical MEO altitude is approximately 20,200 km; this where the U.S. GPS and European Galileo constellations reside. A MEO altitude of ~20,200 km has a ~12 hour orbital period and a constellation of satellites provides global coverage. At this time, about 2% of active satellites are in MEO.
The figure below is a graphical representation of the Galileo global navigation satellite system that is operated by the European Union. One of the aims of the Galileo system is to provide Europe with a high precision positioning system that is independent of the United States GPS (Global Positioning System). The Galileo system has 30 satellites (24 active plus 6 spare) in three MEO planes. The satellites in the U.S. GPS constellation are arranged into six equally-spaced orbital planes surrounding the Earth. Each plane has at least four satellites to ensure that GPS users can view at least four satellites at any time from any place on Earth. As of August 2023, GPS has 31 operational satellites.

Representation of the Galileo global navigation satellites. 30 satellites in three MEO planes. The size of orbits relative to the Earth are approximately to scale but the satellites are depicted much larger than actual size.
Credit: European Space Agency
Geosynchronous Earth Orbit (GSO) and Geostationary Earth Orbit (GEO)
The Geosynchronous Earth Orbit (GSO) altitude is a precise value of 35,786 km. At the GSO altitude, a satellite’s orbital period matches the Earth’s rotation: 23 hours, 56 minutes, and 4.09 seconds, which is termed one sidereal day. The synchronization of orbital period to the Earth’s rotation rate means that a satellite in geosynchronous orbit returns to the same position in the sky after a period of one sidereal day. If a geosynchronous orbits has a non-zero inclination, the satellite will oscillate on a north-south line during the day. A special GSO orbit is the Geostationary Earth Orbit (GEO), also referred to as a geosynchronous equatorial orbit, which has zero inclination and the satellite sits stationary over a particular location of the Earth’s equator. Geostationary orbits are used for satellite distribution of TV signals that enables satellite dishes on homes to be pointed at the geostationary communications satellite (see figure below).
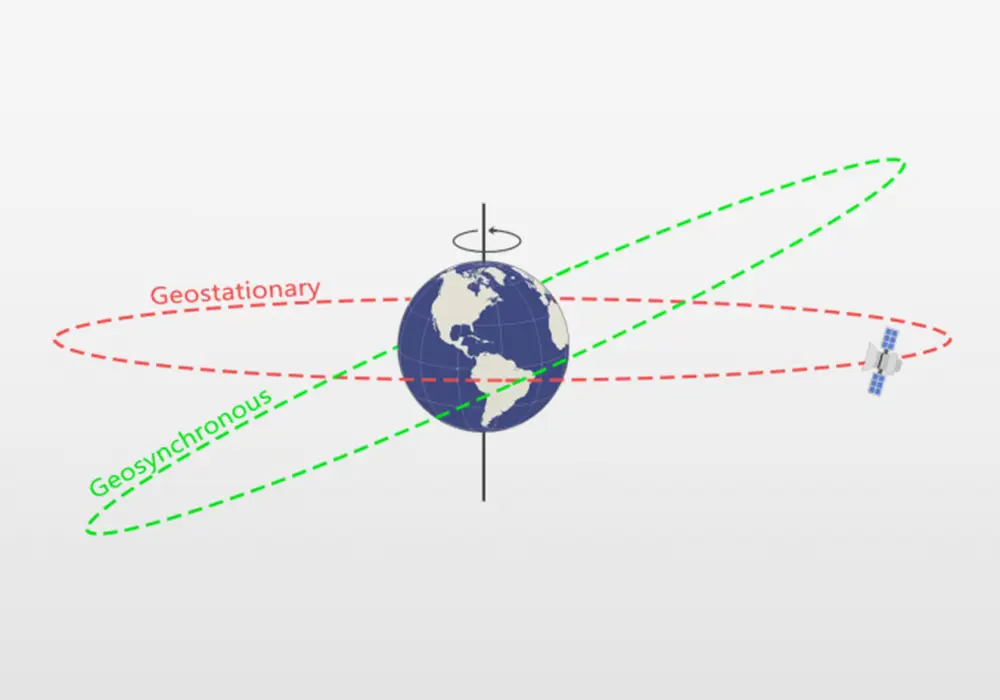
Geosynchronous orbit with nonzero angle of inclination (shown in green) in comparison to the geostationary orbit which has zero angle of inclination (shown in red).
Credit: GISGeography

Home satellite dish pointed to a geostationary satellite orbiting above the Earth’s equator
Photo credit: Allconnect
A very important constellation of Earth Science satellites positioned in geostationary orbit is the Geostationary Operational Environmental Satellite (GOES) constellation. These satellites, developed by NASA and operated by NOAA (National Oceanic and Atmospheric Administration), support weather forecasting, severe storm tracking, and meteorology research . The GOES constellation consists of at least two satellites positioned at longitudes (75°W and 137°W) that provide overlapping views of the continental United States with views of the Atlantic and Pacific oceans to foresee weather systems that impact the United States.
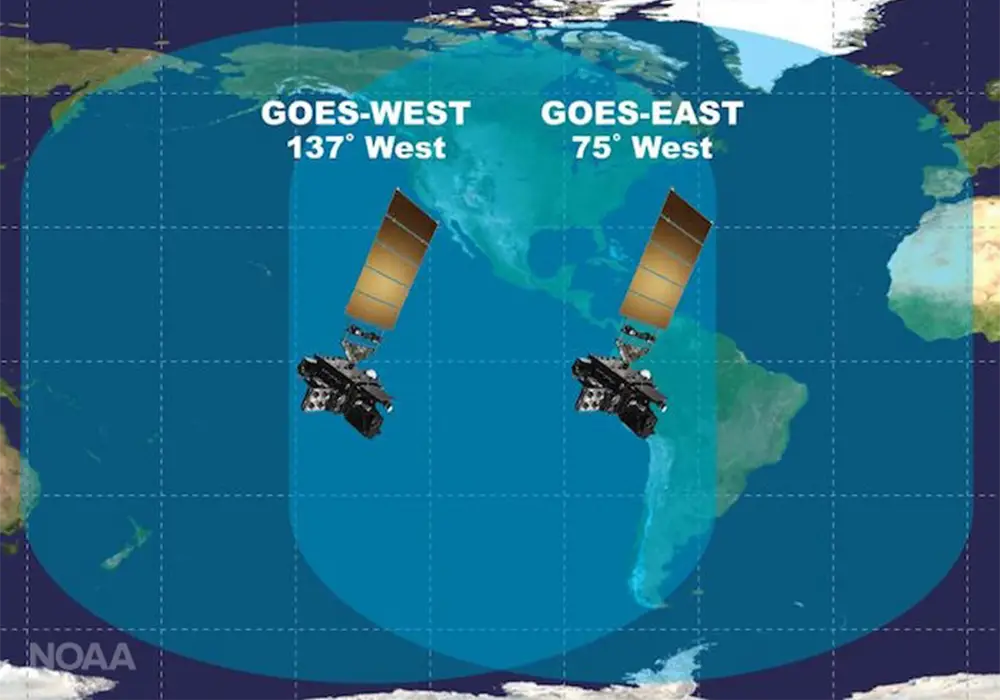
Coverage of the Western Hemisphere by GOES-East and GOES-West
Credit: NOAA
The Japanese Meteorological Agency operates a geostationary satellite similar to GOES which is named Himawari (“sunflower” in Japanese). Himawari is positioned at 140°E longitude, over Japan. Teledyne’s long-wave infrared (LWIR) focal plane arrays are used in the Advanced Baseline Imager (ABI) instruments that operate in the GOES and Himawari satellites.
Highly Elliptical Orbits (HEO)
Geostationary is outstanding for communicating with and observing most of the Earth but geostationary does not have a good view of the Earth’s polar regions. To provide good coverage with long dwell times over the northern polar regions, in the 1960’s, Russia developed the Molniya orbit. A Molniya (“lightning” in Russian) orbit, as shown below, has an inclination angle of 63.4° and high eccentricity (0.722). The Molniya orbit has a 12 hour period during which there are 8 hours that provide a view of the northern polar region. Two satellites in Molniya orbits that are 180⁰ out of phase will provide continuous surveillance coverage of and communication link to the northern polar regions. The specific inclination (63.4°) and eccentricity (0.722) are required to produce the 12 hour orbit period and avoid precession of the orbit (due to the Earth’s oblate spheroid shape).
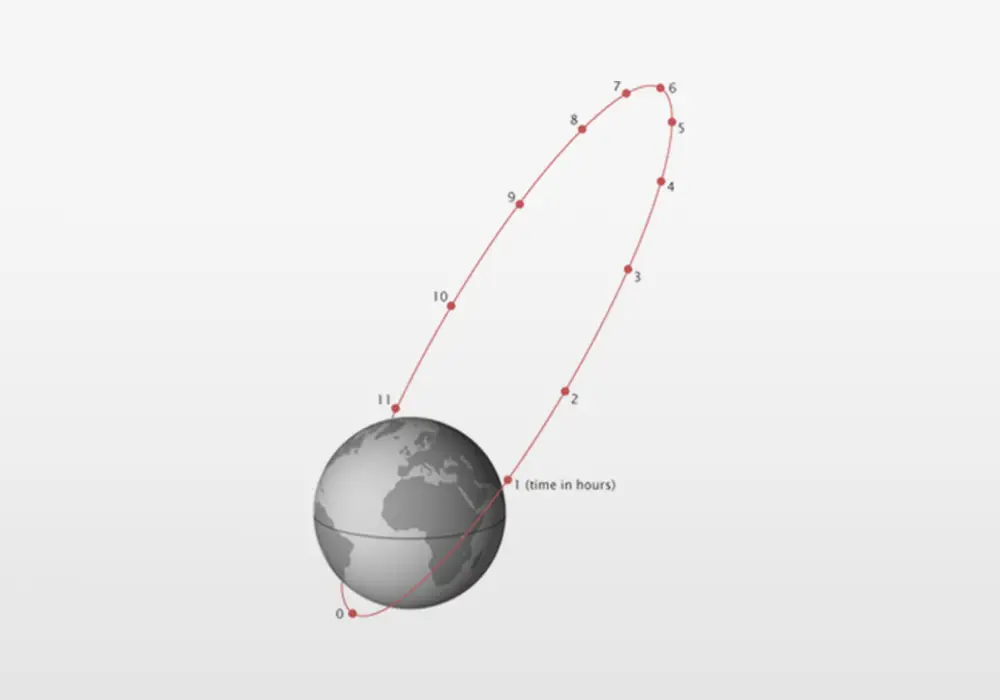
A Molniya orbit has 63.4° inclination and high eccentricity (0.722).
Credit: Wikipedia
Sun-Earth Lagrange Point Orbits
In orbital mechanics there are two special types of orbits. The first one we discussed is the geosynchronous orbit that has an orbital period equal to the rotation of the Earth. The second type is the family of Sun-Earth Lagrange Point orbits. These orbits are special locations where the Sun’s and Earth’s gravity combine to produce a satellite orbit about the Sun that matches the time that it takes the Earth to complete one orbit around the Sun: 365 days, 6 hours, and 9 minutes.
The five Lagrange points are shown in the figure below.
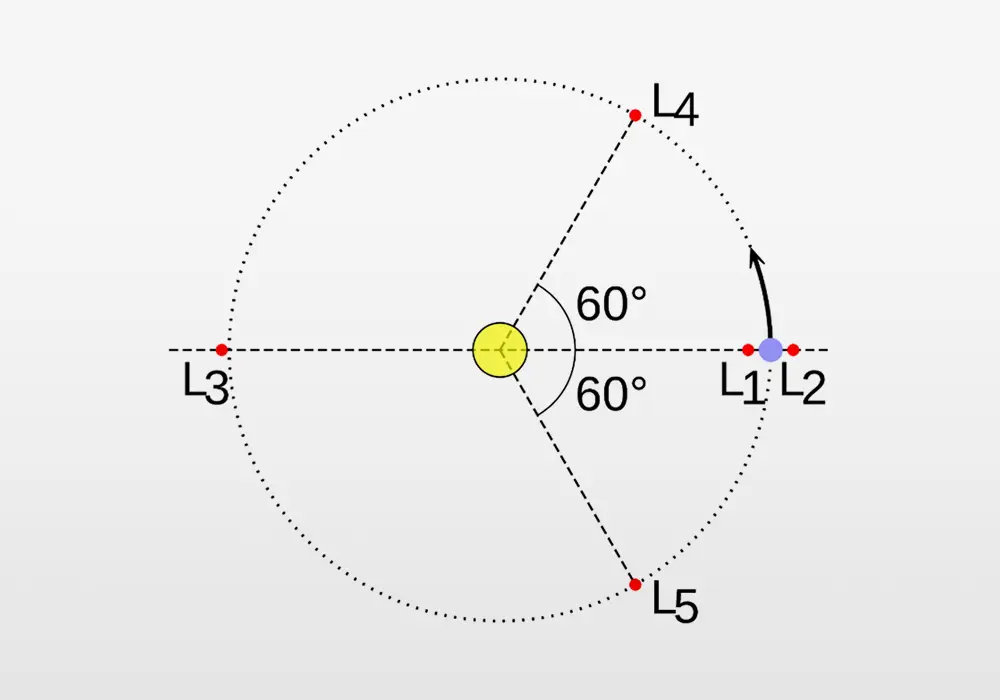
Diagram showing the five Lagrange points in a two-body system with one body far more massive than the other (e.g. the Sun and the Earth).
Credit: Public domain graphic.
When the mass ratio of the two bodies is large enough, the L4 and L5 Lagrange points are stable regions that have a tendency to attract objects. Several planets have asteroids termed “Trojans” that are trapped at their L4 and L5 Lagrange points. Jupiter has more than one million Trojan asteroids and NASA’s Lucy mission is enroute to study 6 Trojan asteroids; the Lucy mission uses Teledyne’s visible and infrared focal plane arrays.
Lagrange point L2 is an excellent location for space astronomy and astrophysics missions since it has lower radiation than LEO and a stable thermal environment that enables 24/7 operation of the mission.
The Lagrange points L1 and L2 are unstable points and satellites must use thruster fuel for “station keeping”. Since Lagrange point L2 lies in the shadow of the Earth, space missions to L2 use a halo orbit about L2 so that the solar panels are constantly illuminated by the Sun (see animation below).
The European Space Agency (ESA) telescope Gaia orbits around Lagrange point L2. Since Lagrange point L2 is exactly in the Earth’s shadow, Gaia does a halo orbit about L2 to receive the sunlight needed to power its solar panels. Every few years, Gaia uses its motors to adjust its position in order to maintain this orbit.
Credit: ESA
Missions located at L2 that use Teledyne’s focal plane arrays include the Gaia mission, the James Webb Space Telescope, the Euclid mission, the PLATO mission (2026 launch), the Roman Space Telescope (2027 launch), and the ARIEL mission (2029 launch).
Lagrange point L1 is a very good location for missions that study the Sun such as NASA’s Solar Dynamics Observatory (SDO). SDO uses Teledyne’s CCD detectors to observe the Sun in ultraviolet wavelengths. L1 is also the best location to search for and characterize near Earth objects (NEOs) that could collide with the Earth. In 2027, NASA plans to launch the NEO Surveyor mission to L1. NEO Surveyor uses Teledyne’s mid-wave and long-wave infrared focal plane arrays to find NEOs (asteroids) that could endanger the Earth.
A visualization of the gravity potentials of the Lagrange points is shown below. Note that Lagrange points L3 and L4 are stable points where there are gravitational wells that will hold a satellite in orbit. L1 and L2 are unstable points that require station keeping.
Visualization of the relationship between the Lagrange points (red) of a planet (blue) orbiting a star (yellow) counterclockwise, and the effective potential in the plane containing the orbit (grey rubber-sheet model with purple contours of equal potential).
Credit: Wikipedia
Interplanetary Orbits
Sending a science mission to the outer solar system requires a lot of energy. Due to the size of the spacecraft and available rocket technology, most missions to the outer solar system use gravity assist maneuvers to slingshot a spacecraft past the inner planets to “steal” some of the planets’ momentum, giving the spacecraft a boost towards its destination. ESA’s JUICE mission requires 3 loops of inner planet flybys and 8 years to reach Jupiter. This section presents animations of two missions that depend on gravity assist:
- NASA’s Lucy mission to Jupiter’s Trojan asteroids
- ESA’s JUICE mission to Jupiter and its moons
NASA Lucy Mission to Jupiter’s Trojan Asteroids
| Launched |
16 October 2021 |
| Earth flyby |
16 October 2022 |
| Asteroid (152830) Dinkinesh flyby |
1 November 2023 |
| Earth flyby #2 |
12 December 2024 |
| Asteroid (52246) Donaldjohanson flyby |
20 April 2025 |
| L4 Trojan asteroid flybys |
12 August 2027 - 11 November 2028 |
| Earth flyby #3 |
25 December 2030 |
| L5 Trojan asteroid flyby |
3 March 2033 |
Lucy mission trajectory shown from multiple angles.
This visualization includes multiple views of the entire Lucy mission in a Jupiter-rotating reference frame. The visualization includes top-down (right), side (bottom left), and oblique (top left) views of the solar system.
Credit: NASA
European Space Agency Jupiter Icy Moons Explorer (JUICE) mission
| Launch |
14 April 2023 |
| Earth-Moon flyby |
August 2024 |
| Venus flyby |
August 2025 |
| Earth flyby #2 |
September 2026 |
| Earth flyby #3 |
January 2029 |
| Arrival to Jupiter |
July 2031 |
| Orbit insertion / Energy Reduction |
July 2031 - June 2032 |
| Science mission Phase |
July 2032 - September 2035 |
JUICE's Journey to Jupiter
Credit: ESA
